3DSpline - Computer Graphics Project

3DSpline, project for subject - Computer Graphics during undergrad.

We were two in a team (Ganesh Pandey and me). And the project basically dealt with making 3D things appear in the screen just by plotting pixels. We could choose any  platform and any programming languages but everything to be done just by plotting pixels in (x, y) of canvas (we could draw lines).

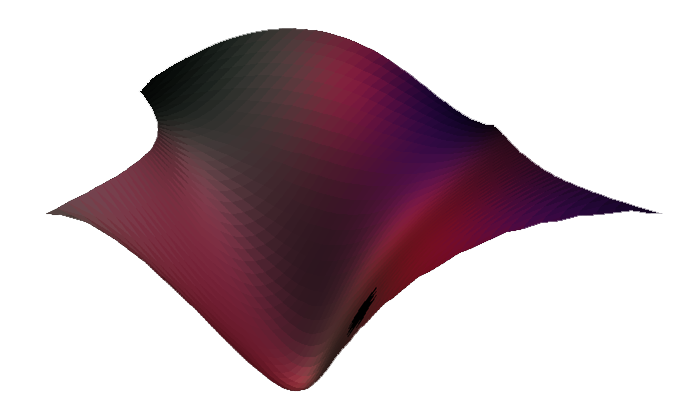
3D surface that we created

3DSpline

To describe the project just in a line – “We made a 3D surface and illuminated it with a bunch of light sources.” The surface can be altered and the lights can be placed anywhere, in any count. We provided a so-called easy interface for the users to alter the shape and position the light sources. The surface can be rotated while keeping the light-sources constant and view the change in illumination.

Components

Surface:

Bezier Surface is the key of our surface co-ordinates. We used a Bezier Surface of third degree which gives us 16 control-points that determines the shape of the surface. For more about Bezier Surface (Read here). We used an input field in UI which gives us the no. of polygons to approximate the surface. Using this parameter, we can evaluate the discrete co-ordinates lying on the surface, thus gave us a finite approximation to our required surface. The control-points for the surface can be made visible and can be dragged to place it anywhere in the space, thus changing the orientation, shape of the surface.

Wireframe of the surface

Light Sources:

The light sources are those which holds colour. The colour appearing in the surface is due to aggregate contribution of individual light source. The colour value of the surface pixel is function of Lambert’s cosine angle and the distance of that pixel with an individual light source. In the project, we implemented this idea to all vertex of polygon. We actually calculated the color value for each vertex rather than every pixels appearing in the surface. And based on this, the rendering techniques for whole surface is dicussed below.

ViewPort:

We have (x,y,z) coordinates for every point. We have a so called imaginary world with fixed position for every vertices of discrete surface. For 3D viewing, we constructed a perspective viewport that transforms 3D objects to 2D perspective. For more about the calculation, read this Wiki.

Methodologies

We used varieties of algorithms coming in our course scope and some others.

Illumination:

As said above, we calculated color-value(intensity) for the vertices of surface polygon. So we evaluated intensities using the vectors.

Given three points in space, we can always find a plane such that it passes through all three points. The equation for the plane can be evaluated using co-ordinates of those three points. Now the equation of plane gives us plane coefficients, which serves as normal vector of the polygon. 

So using this idea, what we exactly needed in our project was to approximate the Bezier surface using polygons bound by three points(triangles). From those boundary points, we can compute normal vector for each of those polygon planes.

But to color the plane, we need intensity contribution by each light source at the vertex points, so that we can interpolate the color within, which means we need vectors for the vertex rather than planes. So to compute the unit normal vector at vertex we evaluated average of the unit vectors of all connected polygons.

Finally, we have approximated unit vector for each vertices which gives us orientation of vertex relative to light source. This is the vector directed from vertex to light source. We can also compute the vector directed from light source to the vertex. Using those two vectors we can evaluate cosine(dot product) to measure at what angle light is incident on that point.

Now the intensity is function of cosine and distance. The contribution from all light sources is evaluated in the same way and finally each vertex comes to have a color.

Shading:

We implemented flat and gourard type of shadings. For flat type, we used the color value of any one vertex to fill the whole polygon and whole surface was painted.

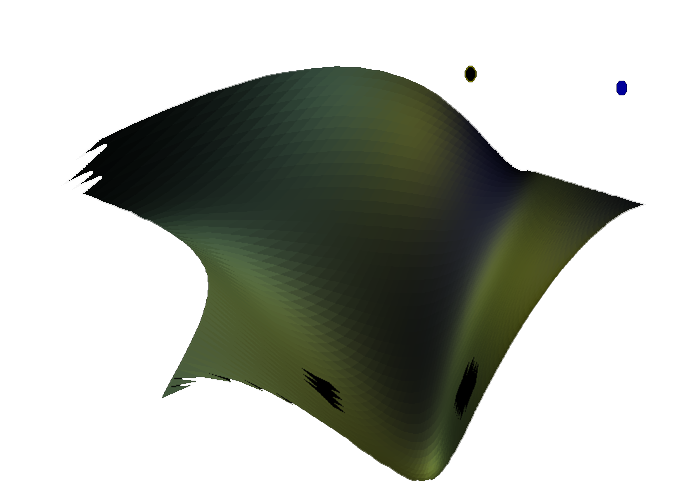
Surface with different sets of color

Surface Painting:

We used an algorithm called ScanLine Polygon fill.

And finally if you are interested with the project, you can fork me on github.